Experiments with a Single Factor - Problems solution
Experiments with a Single Factor
1. A pharmaceutical manufacturer wants to investigate the bioactivity of a new drug.
A completely randomized single-factor experiment was conducted with three dosage levels, and the following results were obtained.
a. Is there evidence to indicate that dosage level affects bioactivity? Use α = 0.05. (Conduct the analysis by hand and then verify the answer by Minitab.
b. If it is appropriate to do so, make comparisons between the pairs of means. What conclusions can you draw?
c. Analyze the residuals from this experiment and comment on model adequacy.
Solution:
a) Is there evidence to indicate that dosage level affects bioactivity? Use α = 0.05. (Conduct the analysis by hand and then verify the answer by Minitab.
We will use the analysis of variance to test
Null hypothesis H0 : µ1 = µ2 = µ3 All means are equal
Alternative hypothesis H1 : µ1 ≠ µ2 ≠ µ3 Not all means are equal
ANOVA: Observations versus Dosage
Factor Type Levels Values
Dosage random 3 20g, 30g, 40g
Analysis of Variance for Observations
Source DF SS MS F P
Dosage 2 450.67 225.33 7.04 0.014
Error 9 2 88.25 32.03
Total 11 738.92
F0.05,2,9 = 4.256 for α = 0.05
Then F0 (7.04) > F0.05,2,9 (4.256 )
So we will accept the alternative hypnosis H1
And there is a difference and evidence affected by dosage level.
b) If it is appropriate to do so, make comparisons between the pairs of means. What conclusions can you draw?
Comparisons between the pairs of means.
Comparisons between the pairs of means.
Using Tukey’s Test:
Equal variances were assumed for the analysis.
q0.05( p, f ) = q0.05( 3, 9 ) = 3.95 from Percentage Points of the Studentized Range Statistic
Thus, any pairs of treatment averages that differ in absolute value by more than 11.1775 would imply that the corresponding pair of population means are significantly different.
The differences in averages are:
Then from Tukey’s Test for pairs comparison we find that the pair of dosage 20 g and 40 g is the most effective.
using Minitab:
Model Summary
S = 5.65931 R-Sq = 60.99% R-Sq(adj) = 52.32% R-sq(pred)= 30.65%
Dosage N Mean StDev 95% CI
20g 4 29.75 5.44 (23.35, 36.15)
30g 4 36.75 5.44 (30.35, 43.15)
40g 4 44.75 6.08 (38.35, 51.15)
Pooled StDev = 5.65931
Tukey Pairwise Comparisons
Grouping Information Using the Tukey Method and 95% Confidence
Dosage N Mean Grouping
40g 4 44.75 A
30g 4 36.75 A B
20g 4 29.75 B
Tukey Simultaneous Tests for Differences of Means
Difference Difference SE of Adjusted
of Levels of Means Difference 95% CI T-Value P-Value
30g - 20g 7.00 4.00 (-4.18, 18.18) 1.75 0.240
40g - 20g 15.00 4.00 ( 3.82, 26.18) 3.75 0.011
40g - 30g 8.00 4.00 (-3.18, 19.18) 2.00 0.168
Individual confidence level = 97.91%
c) Analyze the residuals from this experiment and comment on model adequacy.
Compute the residuals for each observation:
eij = yij - 𝑦 ̅i.
ӯ1. | ӯ2. | ӯ3. |
29.75 | 36.75 | 44.75 |
20g | 20gresiduals | 30g | 30gresiduals | 40g | 40gresiduals | |
1 | 24 | -5.75 | 37 | 0.25 | 42 | -2.75 |
2 | 28 | -1.75 | 44 | 7.25 | 47 | 2.25 |
3 | 37 | 7.25 | 31 | -5.75 | 52 | 7.25 |
4 | 30 | 0.25 | 35 | -1.75 | 38 | -6.75 |
the central values closely fit a straight line, the errors are normally distributed and the model is adequate.
------------------------------
2. Four chemists are asked to determine the percentage of methyl alcohol in a certain chemical compound. Each chemist makes three determinations, and the results are the following:
a. Do chemists differ significantly? Use α = 0.05.
b. Analyze the residuals from this experiment.
c. If chemist 2 is a new employee, construct a meaningful set of orthogonal contrasts that might have been useful at the start of the experiment.
Solution:
a) Do chemists differ significantly? Use α = 0.05.
Using Minitab:
ANOVA:
Factor Levels Values
Chemist 4 1, 2, 3, 4
Analysis of Variance
Source DF Adj SS Adj MS F-Value P-Value
Chemist 3 1.0446 0.3482 3.25 0.081
Error 8 0.8582 0.1073
Total 11 1.9028
Model Summary
S R-sq R-sq(adj) R-sq(pred)
0.327529 54.90% 37.98% 0.00%
Means
Chemist N Mean StDev 95% CI
1 3 84.470 0.481 ( 84.034, 84.906)
2 3 85.0533 0.1504 (84.6173, 85.4894)
3 3 84.787 0.345 ( 84.351, 85.223)
4 3 84.283 0.236 ( 83.847, 84.719)
Pooled StDev = 0.327529
F0.05,3,8 = 4.066 for α = 0.05
Then F0 (3.25 ) < F0.05,3,8 ( 4.066 )
So we will accept the null hypnosis Ho and there is no difference at α = 0.05
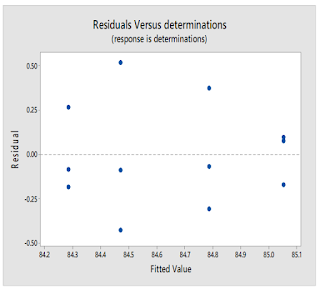
b) Analyze the residuals from this experiment.
Compute the residuals for each observation:
eij = yij - 𝑦 ̅i.
ӯ1. | ӯ2. | ӯ3. | ӯ4. |
84.47 | 85.05333 | 84.78667 | 84.28333 |
1 | residuals | 2 | residuals | 3 | residuals | 4 | residuals | |
1 | 84.99 | 0.52 | 85.15 | 0.096667 | 84.72 | -0.06667 | 84.2 | -0.08333 |
2 | 84.04 | -0.43 | 85.13 | 0.076667 | 84.48 | -0.30667 | 84.1 | -0.18333 |
3 | 84.38 | -0.09 | 84.88 | -0.17333 | 85.16 | 0.373333 | 84.55 | 0.266667 |
The central values closely fit a straight line, the errors are normally distributed and the model is adequate.
c) If chemist 2 is a new employee, construct a meaningful set of orthogonal contrasts that might have been useful at the start of the experiment.
Orthogonal contrasts = a - 1 = 3
Chemist 2 is a new employee
C1 : µ2 = (µ1 + µ3+ µ4 )
C2 : µ1 +µ3 = µ4
C3 : µ3 = µ4
Hypothesis Contrast:
Chemist | Totals | C1 | C2 | C3 |
1 | 253.41 | 1 | 1 | 0 |
2 | 255.16 | -3 | 0 | 0 |
3 | 254.36 | 1 | 1 | 1 |
4 | 252.85 | 1 | -2 | -1 |
-4.86 | 2.07 | 1.51 |
At 5% significance level
the SSC has only one degree of freedom, we know that SSC = MSC.
The relevant test statistics:
the critical value is F0.05,3,11 = 3.59.
C1 is the only contrast test statistic that is greater than the critical value.
So, the only contrast that useful at the start of the test at a 5% significance level is contrast 1.
------------------------------
Labels:
Education